Twój koszyk jest obecnie pusty!
| Lee Sedol zapalił papierosa na hotelowym tarasie. Potrzebował przerwy. Chwilę wcześniej, w niewielkiej sali konferencyjnej, na jasnej, masywnej, drewnianej tablicy położył kolejny biały kamień. Wykonał trzydziesty szósty ruch drugiej partii meczu Go. Miliony obserwowały, jak przegrał pierwszą z pięciu zaplanowanych partii. Drugą musiał wygrać. Był jednym z najsilniejszych graczy na świecie, prawdopodobnie nawet najsilniejszym. Był 10 marca 2016 roku. Przeciwnik – stworzony przez DeepMind program AlphaGo – wykonał ruch numer 37. |
Świat, człowiek, AI i Go
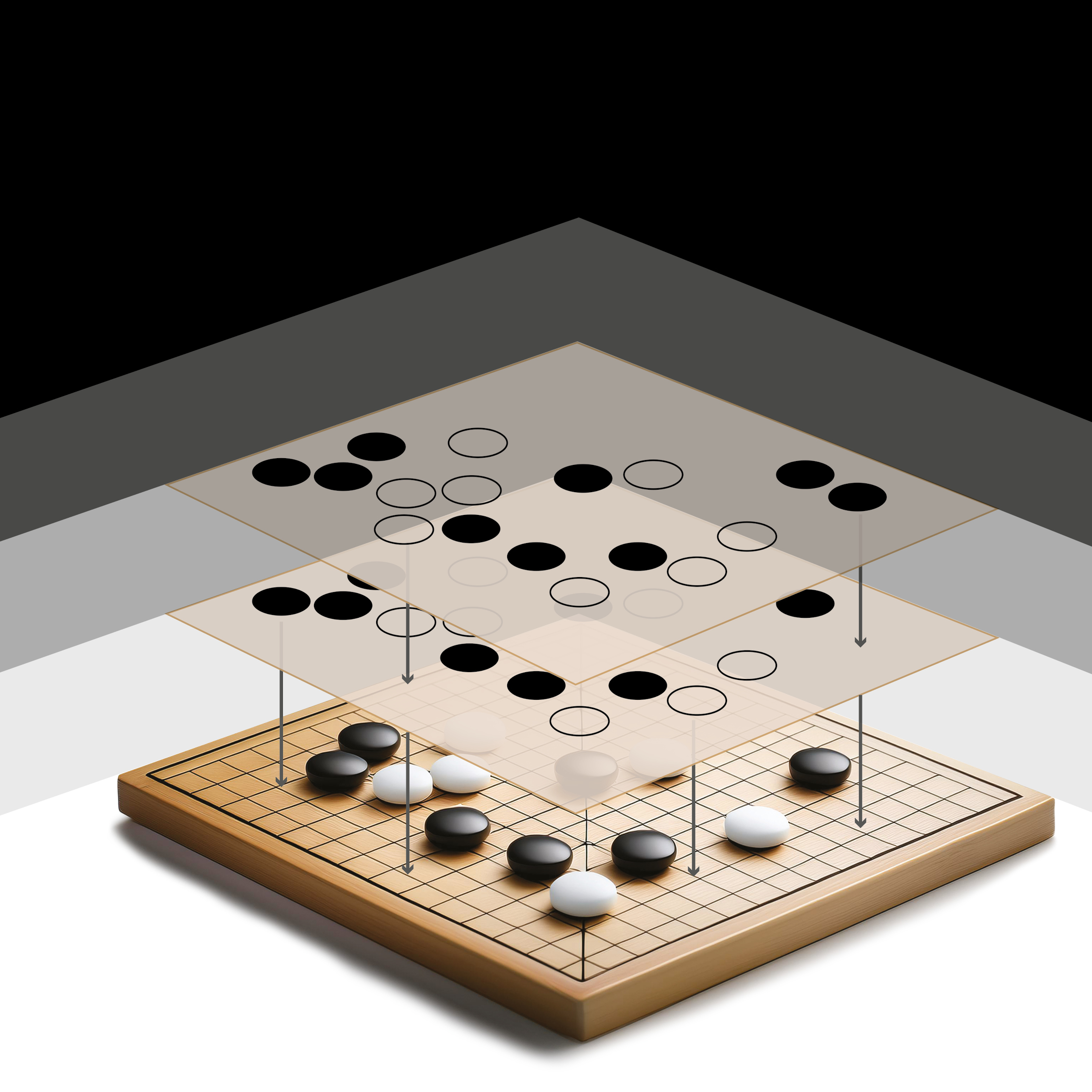
Reguły Go są proste. Na tablicy przeciętej dziewiętnastoma pionowymi i poziomymi liniami dwóch graczy układa na przemian czarne i białe kamienie . Wygrywa ten, kto otoczy kamieniami większe terytorium. Te proste reguły składają się jednak na niewyobrażalną złożoność rozgrywki. Go zachwyca nią ludzi od ponad dwóch i pół tysiąca lat. Liczba możliwych dozwolonych konfiguracji kamieni jest podobno większa od szacowanej liczby atomów w obserwowalnym wszechświecie.
Podobnie jest w matematyce. Z kilku prostych aksjomatów i wybranych zasad wnioskowania rodzą się nieskończone przestrzenie i struktury, które pozwalają doskonale opisać lub odgadnąć prawa rządzące naszym światem. Podobnie sprawy mają się w sztuce i w życiu.
Skuteczne poruszanie się po stwarzającej takie możliwości przestrzeni wymaga czegoś więcej niż umiejętność stosowania się do panujących reguł. Wymaga głębokiego ich rozumienia, przewidywania konsekwencji, twórczego ich wykorzystywania oraz zdolności poszukiwania nowych rozwiązań. Dzięki naszej kreatywności, wyobraźni, intuicji i ciekawości możemy być w tym bardzo dobrzy.
Czy równie dobry może być w tym algorytm? Czy ludzki sposób rozumowania oparty na wszystkich wyżej wymienionych umiejętnościach można zapisać w postaci równania lub właśnie algorytmu? Jeśli tak, to być może możliwe byłoby również stworzenie sztucznej inteligencji, która dorównywałaby człowiekowi. Tylko jak to sprawdzić?
Potrzebny byłby nam świat przynajmniej tak samo złożony jak otaczająca rzeczywistość, ale jednocześnie opisany prostymi regułami, które można zaprogramować. Świat, w którym można umieścić uczącą się bez udziału człowieka wirtualną istotę. Świata, do którego dostęp powinien mieć także człowiek. Tak, abyśmy mogli porównać jego kreatywność, wyobraźnię, intuicję i ciekawość z tą wirtualną. Najlepiej poprzez współzawodnictwo. Ready, steady, Go!
Strategia gry
| Lee ze zdziwieniem patrzył na tablicę, na której pojawił się nowy czarny kamień. Doświadczenie pokoleń graczy podpowiadało, że ruch AlphaGo był błędem. Tak się nie grało. Takiego ruchu nie wykonałby człowiek, który miałby możliwość zmierzenia się z mistrzem Lee Sedolem. Lee poczuł jednak coś dziwnego. Tracił kontrolę nad przebiegiem rozgrywki. |
Algortym AlphaGo jest algorytmem sterowania, który poszukuje przybliżonego (dobrego) rozwiązania problemu wieloetapowego podejmowania decyzji w warunkach niepewności.
A teraz bardziej po ludzku: wyobraźmy sobie, że jedziemy na spotkanie i jesteśmy już trochę spóźnieni. Musimy jak najszybciej dotrzeć na drugi koniec miasta, a z jakichś przyczynnie mamy dostępu do nawigacji. Przed nami kilka skrzyżowań. Na każdym musimy zdecydować, którą drogą pojechać. Co bierzemy pod uwagę?
Po pierwsze, to co mamy przed oczami. Widzimy jak wygląda trasa do kolejnego skrzyżowania, widzimy czy jest zakorkowana czy nie, i oceniamy koszt przejechania tego krótkiego odcinka.
Po drugie, oczywiście to, czego nie widzimy. Na bieżąco oceniamy całkowity czas, jaki zajmie nam dojazdu do celu trasą, którą obraliśmy. Tą, którą widzimy oczyma wyobraźni. Z doświadczenia wiemy, które z tras są lepsze, które gorsze. To przecież nasze miasto. Możemy wybrać szybki przejazd do kolejnego skrzyżowania i potem stać w długim korku. Albo możemy najpierw skręcić w uliczkę, która może i jest zatłoczona, ale pozwoli nam ominąć korek. Każda decyzja niesie za sobą konsekwencje. Ciąg decyzji podejmowanych na kolejnych skrzyżowaniach wyznaczy trasę i czas naszego przejazdu.
Jeśli jechalibyśmy przez puste miasto, pojechalibyśmy prosto do celu. Jednak w godzinach szczytu każde skrzyżowanie stwarza nam wybór. I na każdym musimy szacować konsekwencje tych wyborów. Świadomie lub nie, stosujemy jakąś regułę.
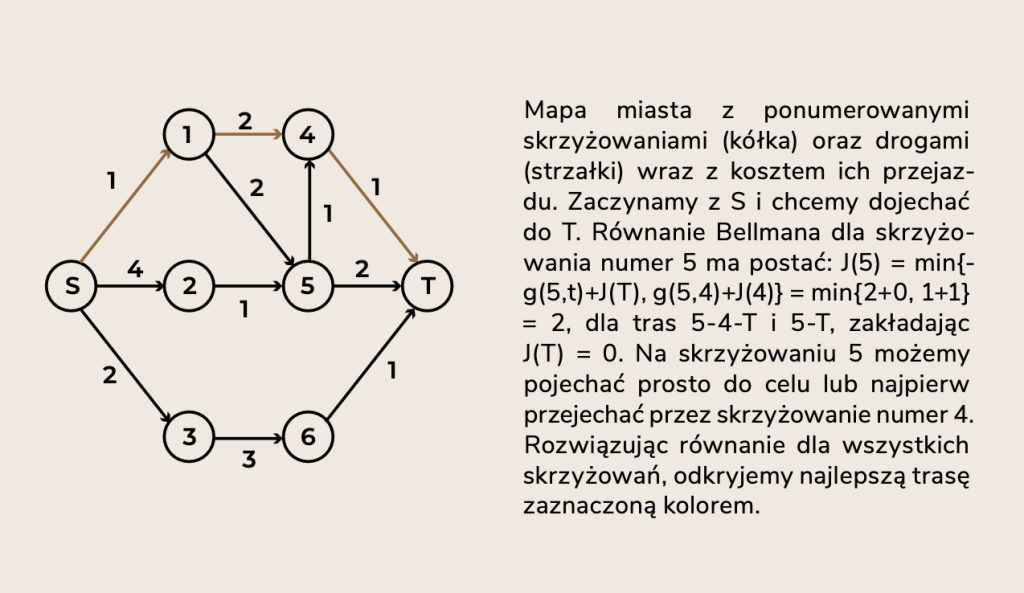
Podobny problem rozwiązywał AlphaGo. Obserwował aktualny stan tablicy, wybierał ruch, który wydawał się mu zarówno dobrą odpowiedzią na układ kamieni, jak i maksymalizował szanse na wygraną. W przypadku Go problem ten jest oczywiście niewyobrażalnie bardziej złożony. Skrzyżowań (układów kamieni) są przerażające ilości, miejsce spotkania (korzystny podział terytorium) zmienia się co chwila, a korki (ruchy przeciwnika) zmieniają mapę miasta nie do poznania.
To zachwycające, że udało nam się tak dobrze opanować tę rozgrywkę. Lee był w tym mistrzem. Podobnego poziomu nie był w stanie osiągnąć żaden program komputerowy. Wyglądało na to, że kreatywność, wyobraźnia, intuicja i ciekawość to coś więcej niż algorytm, i to my na te supermoce mamy monopol.
Sekwencję kolejno stosowanych reguł podejmowania decyzji nazywamy strategią (lub polityką) sterowania. AlphaGo musiał najpierw nauczyć się grać w grę i opracować własną strategię.
Jak nauczyć się dobrze grać?
Skonstruowanie najlepszej możliwej strategii jest piekielnie trudne, ale znamy na nią przepis. Ot, matematyka.
Załóżmy, że znamy optymalną strategię jazdy przez miasto. Przenieśmy się teraz na sam koniec trasy i spójrzmy na najbliższe skrzyżowania. Mogliśmy dotrzeć do celu z dowolnego z nich. Optymalna reguła sterowania, którą wykorzystalibyśmy na ostatnim etapie podróży, wskaże nam najlepszą trasę z dowolnego skrzyżowania prowadzącego bezpośrednio do celu. Tu sprawa jest prosta, wybór jest niewielki. Poznamy jednak koszty optymalnych decyzji na tym etapie, co jest szczególnie ważne.
Zróbmy teraz kolejny krok wstecz. Do celu musimy pokonać dwa skrzyżowania, to na którym jesteśmy i to ostatnie, prowadzące bezpośrednio do celu. Tutaj mamy większy wybór i musimy na poważnie liczyć się z konsekwencjami. Musimy wziąć pod uwagę dwa składniki kosztu: koszt dojechania do najbliższego skrzyżowania oraz koszt dalszej podróży. To właśnie zrobi optymalna reguła, wybierze najmniejszy całkowity koszt dojazdu do celu z dowolnego skrzyżowania, na którym się znajdziemy na tym etapie. Ale jak oceni konsekwencje swoich decyzji, jak je sobie wyobrazi? Nic prostszego! Gdziekolwiek trafimy, znamy już przecież optymalne koszty na ostatnim etapie!
I tak dalej, to znaczy wstecz, od końca do początku podróży.
Ogony strategii optymalnej, czyli reguły postępowania od wybranego etapu pośredniego do etapu końcowego, są optymalne dla każdego stanu początkowego. Tak brzmi słynna i potężna zasada optymalności odkryta w latach ‘50 przez Richarda E. Bellmana. To jest nasz przepis, równanie Bellmana:
$J_k(x) = \min \mathbb{E}\{g_k(x,u,w)+J_{k+1}(f(x,u,w))|\ u\in U_k, w\sim P(x,u)\}$
W zaklęciu tym $x$ oznacza stan, w którym się znajdujemy, $u$ decyzję do pojęcia, a $w$ zewnętrzne losowe przeszkody. Funkcja $f(x,u,w)$ to model świata. Mówi nam dokąd trafimy ze stanu $x$, jeśli zrobimy ruch $u$, a potem wydarzy się $w$ z prawdopodobieństwem $P(x,u)$. Funkcja $g_k(x,u,w)$ to koszt tego zdarzenia na etapie $k$. Na każdym etapie wolno nam wybierać jedynie ruchy ze zbioru $U_k(x)$. Napis $\min \mathbb{E}$ oznacza, że dla każdej decyzji $u$ obliczamy średni szacowany koszt całej zabawy i wybieramy ten najmniejszy (czyli znajdujemy najlepszą decyzję).
Na koniec najważniejszy element. Funkcja $J_k(x)$ jest wskaźnikiem jakości stosowania strategii optymalnej. Mówi ona, jakie konsekwencje poniesiemy, gdy w etapie $k$ znajdziemy się w stanie $x$, a potem będziemy stosować strategię optymalną.
Jeżeli znamy wszystkie konsekwencje każdej możliwej decyzji podejmowanej w ciągu całej rozgrywki, to strategia optymalna jest zbudowana z reguł:
$\mu_k(x) \in \arg\min \mathbb{E}\{g_k(x,u,w)+J_{k+1}(f(x,u,w))|\ u\in U_k, w\sim P(x,u)\}$
W etapie $k$ strategia optymalna wybiera decyzję, która jest wartością funkcji $\mu_k$ w stanie $x$. Decyzja ta niesie ze sobą najlepsze możliwe konsekwencje, od chwili $k$ do końca rozgrywki. Uwaga, musimy znać sekwencję funkcji $J_k(x)$, żeby zastosować powyższy algortym. You’re welcome!
W praktyce jest tak, że często nie znamy liczby etapów, albo proces decyzyjny może się wielokrotnie powtarzać. Zakładamy więc dla uproszczenia, że zabawa trwa w nieskończoność. To jedno z ulubionych uproszczeń w matematyce. Często zależy nam również na maksymalizacji wyników, np. prawdopodobieństwa zwycięstwa w meczu Go. Wtedy równanie Bellmana przyjmuje taką postać:
$J(x) = \max Q(x,u) = \max \mathbb{E}\{g(x,u,w)+\alpha J(f(x,u,w))|\ u\in U(x), w\sim P(x,u)\}$
Przepis na optymalną strategię? Wybieramy kolumnę $u$ zawierającą najlepszą wartość w wierszu $x$ tabeli $Q(x,u)$, czyli:
$\mu(x) = \arg \max Q(x,u)$
Możemy, stop, musimy również uwzględnić nagrodę $D(x,u)$ za ciekawość eksploracji ruchów $u$ wcześniej niezbadanych, czyli
$\mu(x) = \arg \max Q(x,u) + D(x,u)$
Taki właśnie problem rozwiązano budując najsilniejsze wcielenie algorytmu AlphaGo. W ten sposób sam siebie zbudował AlphaGo Zero. Do czego dojdziemy już za chwilę.
I mamy przepis na optymalną strategię! To w czym problem?
Złożoność gry w Go. Nie da się efektywnie rozwiązać równania Bellmana, gdy możliwości jest tak wiele. Nie pomoże w tym żaden klaster wypchany po brzegi kartami z GPU.
Równanie Bellmana musi być prawdziwe dla każdego stanu. Zatem, w procesie jego rozwiązywania dla każdego stanu musimy rozwiązać skomplikowane zadanie obliczeniowe, musimy znać model świata oraz rozkład prawdopodonieństwa zdarzeń losowych, o estymacji ostatecznych wyników nie wspominając. Z praktycznego punktu widzenia to tak złożone, że niemożliwe. Równanie Bellmana jest dotkliwie dotknięte przekleństwem wymiarowości.
Zatem jakim cudem potrafimy tak dobrze grać w Go? Dzięki wyobraźni, intuicji i ciekawości.
Wyobraźnia, intuicja i ciekawość, czyli Reinforcement Learning
Lee Sedol i Dennis Hassabis, założyciej DeepMind i współtwórca algortymu AlphaGo, mrużyli oczy od błysków zdjęć siedzących przed nimi dziennikarzy. AlphaGo wygrał drugą partię. Lee podniósł mikrofon. “Wczoraj byłem zaskoczony. Dzisiaj brakuje mi słów. Jestem w szoku. AlphaGo zagrał prawie doskonałą grę.” Ruch numer 37 przeszedł do historii, bo okazał się kluczowy dla zwycięstwa. Pokazał nową strategię, której nie udało się odkryć pokoleniom mistrzów. AlphaGo był nowatorski i twórczy. Pokonał człowieka.
Demis Hassabis i Mustafa Suleyman założyli DeepMind w 2010 roku, żeby stworzyć pierwszy w historii algorytm wygrywający z człowiekiem w Go. Chcieli udowodnić, że można zaprogramować proces uczenia podobny do ludzkiego i w ten sposób stworzyć model AI podejmujący decyzje lepiej od człowieka. Sześć lat później osiągnęli ten cel. A kluczem było zwycięstwo nad przekleństwem wymiarowości równania Bellmana. Na jakich założeniach się opierało?
Po pierwsze, nie potrzebujemy optymalnej strategii gry. Wystarczy nam dobra strategia, którą będziemy mogli poprawiać lub wzmacniać na podstawie obserwowanych interakcji z otoczeniem.
Po drugie, nie musimy znać wszystkich konsekwencji wszystkich możliwych decyzji. Wystarczą nam prognozy konsekwencji tych sensownych. I to tylko tych, które malują się na niezbyt odległym horyzoncie. Wystarczy, że wyobrazimy sobie, co mogłoby się wydarzyć i dostaniemy nagrodę za trafioną prognozę.
Po trzecie, musimy znaleźć sensowny kompromis pomiędzy ciekawością i doświadczeniem, exploit or explore?
Tyle wystarczy. Wyobraźnia, chęć uczenia się, intuicja oraz ciekawość. W nagrodę dostajemy kod źródłowy kreatywności.
Taki sposób konstruowania strategii lub uczenia maszynowego, nosi nazwę uczenia przez wzmacnianie, czyli Reinforcement Learning (RL).
Monte Carlo w lesie
| Lee wiedział, że AlphaGo przewyższa go zdolnością analizowania niezliczonych scenariuszy gry, a także zdolnością prognozowania konsekwencji ruchów. Wiedział, jak – dzięki nadludzkiej wyobraźni – kreatywna może być jego gra. A gdyby tak zrobić coś szalonego? – pomyślał. Lee położył na tablicy kamień numer 78. AlphaGo katastrofalnie zahalucynował. |
Algorytm RL obserwuje aktualną strategię gry i nieustannie ją poprawia, wzmacnia dobre reakcje i tłumi złe. Robi to szacując konsekwencje decyzji oraz umiejętnie ważąc ciekawość eksploracji ze zdobytym doświadczeniem. Może zacząć nawet od losowego zestawu reguł i jakiegoś wyobrażonego szacunku ich konsekwencji. A w procesie uczenia, stopniowo, krok po kroku, strategia będzie stawała się coraz lepsza.
Przełomem było złożenie ofiary z optymalności i wszechwiedzy zaszytych w równaniu Bellmana:
$\tilde{\mu}_k(x) \in \arg\max \tilde{Q}_{k}(x,u) = \mathbb{E}_{w}\{g_k(x,u,w)+\tilde{J}_{k+1}(f(x,u,w)) |\ u\in \tilde{U}_k, u_{k+n}\sim\tilde{\mu}_{k+n}\}$
Najpierw oczywiście sprawdzamy, w jakim stanie $x$ jesteśmy i co sensownego $u\in \tilde{U}_k$ możemy zrobić. Następnie, wyciągamy z rękawa jakiś zestaw rozsądnych i intuicyjnie dobrych reguł $\tilde{\mu}_{k}$. Nazwiemy je strategią bazową. To tę strategię będziemy poprawiać poprzez planowanie jednego ruchu do przodu, tzw. lookahead (chociaż moglibyśmy oczywiście planować również kilka ruchów do przodu). A potem wielokrotnie stosujemy strategię $\{u,\tilde{\mu}_{k+1},…,\tilde{\mu}_{k+N}\}$, tzw. rollout, symulując po drodze odpowiedzi $w$ przeciwnika (lub wielu różnych przeciwników) w kolejnych ruchach.
Losowe generowanie wyników gry utworzy drzewo wariantów rozgrywki, a liście tego drzewa będą zawierały jej szacowany rezultat. Taka procedura eksplorowania możliwości nosi nazwę Monte Carlo Tree Search (MCTS). Nie jest to byle losowa eksploracja. Procedura notuje popularność gałęzi odwiedzanych przez strategię bazową, dzięki czemu pozwala rozwiązać problem exlore/exploit. Przy wyborze decyzji możemy uwzględnić nie tylko konsekwencje, ale także ciekawość zbadania dotychczas niezbadanych ścieżek.
Uśredniony wynik symulacji MCTS zwraca prognozę wyniku, który jest zapisywany w tabeli $\tilde{Q}_k(x,u)$. Liczba na przecięciu wiersza $x$ i kolumny $u$ oznacza szacowany rezultat decyzji $u$ w stanie $x$. Wybór optymalnej polega więc na wyborze kolumny, która w wierszu $x$ zawiera najlepszą wartość. Takie $\tilde{u}$ zapisujemy następnie jako wartość nowej reguły decyzyjnej $\tilde{\mu}_k(x)$. Wykonanie ruchu $u=\tilde{\mu}_k(x)$ przeniesie nas do kolejnego stanu. W nim ponownie wykonamy powyższe kroki.
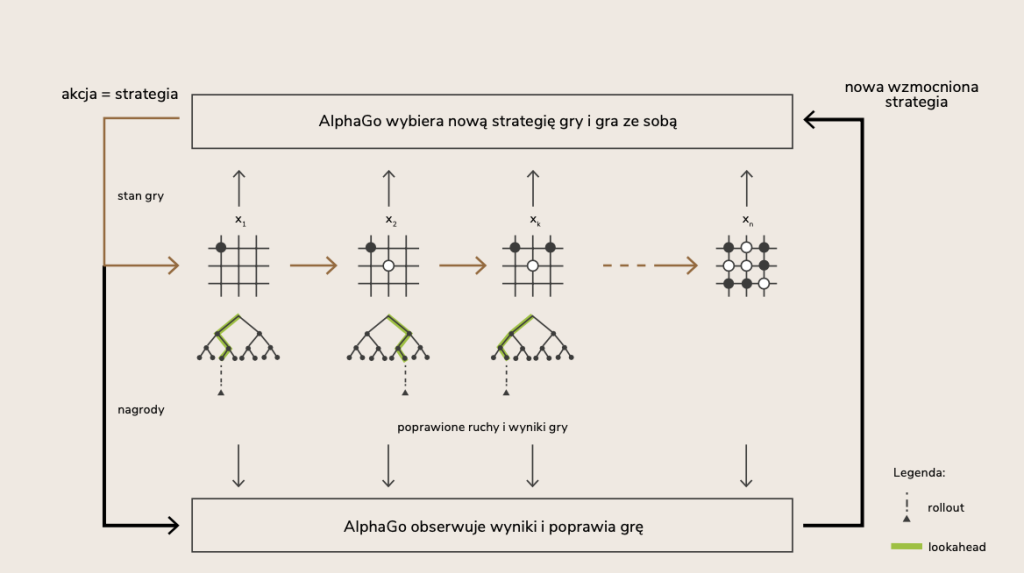
Wybór i rozbudowa scenariusza (lookahead), symulacja (rollout) i aktualizacja ocen (backup/update) to podstawowe kroki procesu. Poprzez wielokrotne ich wykonywanie poprawiamy strategię bazową! Jednocześnie poprawiamy także prognozy konsekwencji naszych ruchów.
Rozbudowaną wersję (nieskończony horyzont) tego podejścia zastosowano w trenowaniu AlphaGo. Strategię bazową złożono z dwóch sieci neuronowych, większej i mniejszej (policy network), wytrenowanych na bazie ruchów graczy ekspertów (ludzkich). Sieci te miały przewidywać prawdopodobieństwo następnego ruchu (człowieka) w określonej konfiguracji kamieni.
Większa sieć rozwijała scenariusz gry po sekwencji ruchów eksplorujących (lookahead). Mniejsza doprowadzała grę do końca (rollout). Algorytm MCTS estymował rezultaty gier, które wielokrotnie prowadzone były w ten sposób przeciwko poprzedniej wersji strategii bazowej. Do estymacji rezultatów wykorzystano konwolucyjną sieć neuronową (value network), która obraz kamieni na tablicy tłumaczyła na szansę wygranej. Strategię wzmacniano według reguły
$\mu(x) = \arg\max Q(x,u) + D(x,u)$,
promując ciekawość eksploracji nagrodą $D(x,u)$.
AlphaGo grał sam se sobą. Ucząc się na swoich błędach. I katastrofalnych halucynacjach.
AlphaZero, AlphaFold, AlphaProof, AlphaOmega?
| Lee wygrał tylko jedną z pięciu zaplanowanych gier. Ruch numer 78 wykonany przez niego w czwartej grze był dla AlphaGo tym, czym ruch 37 był dla człowieka. Źródłem inspiracji do nauki i wzmocnienia strategii. Piąta gra znów należała do AI. |
AlphaGo vs Człowiek, 4-1.
| Lee głęboko przeżył tę porażkę. Karierę zawodową zakończył wkrótce potem, 19 listopada 2019 roku. Po przejściu na emeryturę (ma 41 lat) zainteresował się projektowaniem gier planszowych. |
Kariera AlphaGo także dobiegła końca.
Doświadczenia zgromadzone przez DeepMind doprowadziły do powstania AlphaGo Zero, najsilniejszej wersji algorytmu. W tym przypadku nie wykorzystywano już wiedzy człowieka. AlphaGo Zero sam nauczył się gry w Go, wielokrotnie grając ze sobą. Osiągnął nadludzki poziom.
AlphaGo Zero vs AlphaGo, 100-0.
Strategia bazowa oraz prognoza rezultatu gry tym razem zostały zamodelowane przy pomocy jednej sieci neuronowej, która na wejściu otrzymywała obraz, układ kamieni. Na wyjściu zwracała rozkład prawdopodobieństwa ruchów oraz ocenę prawdopodobieństwa wygranej. Za wzmacnianie strategii wciąż odpowiadał algorytm MCTS, jednak bez kroku rollout. Ruchy eksplorujące wykonywane były przez aktualną wersję strategii, a następnie były poprawiane (lookahead) na podstawie prognoz wyniku. Obserwacje tych ruchów i uzyskanych wyników wykorzystywano jednocześnie do trenowania sieci.
Krok po kroku, algorytm RL zbliżał AlphaGo Zero do doskonałego rozwiązania równania Bellmana.
“Ludzkość zgromadziła wiedzę o Go z milionów partii, które zostały rozegrane na przestrzeni tysięcy lat, wiedzę skondensowaną w postaci wzorców, reguł i książek. W ciągu zaledwie kilku dni, zaczynając od zera (tabula rasa), AlphaGo Zero zdołało ponownie odkryć znaczną część tej wiedzy o Go, a także wypracować nowe strategie, które dostarczają świeżego spojrzenia na jedną z najstarszych gier świata.”
Silver et al., Mastering the game of go without human knowledge. Nature (2017).
Co stało się potem? Ewolucja napędzana przez RL stworzyła AlphaZero, model samodzielnie uczący się grać w Go, szachy, Shogi, lub dowolną grę logiczną dla dwóch graczy. Model, który gra na poziomie przewyższającym możliwości człowieka.
A potem? Powstał AlphaFold, model przewidujący strukturę przestrzenną białka na podstawie sekwencji jego aminokwasów. Model dający nadzieję na niezwykłe przyspieszenie procesu odkrywania leków i tłumaczenia przyczyn chorób.
A potem? AlphaProof nauczył się formalnego matematycznego wnioskowania i rozwiązał poprawnie trzy z sześciu zadań Międzynarodowej Olimpiady Matematycznej 2024, osiągając poziom srebrnego medalisty.
A potem?