Neural networks from scratch

Leading contemporary artificial intelligence algorithms rely on computations based on certain mathematical patterns. The simplest models can be based on just one equation, while the most complex ones rely on a set of thousands of interdependent equations. The complexity of the calculations is closely related to the potential of the algorithm. This is due to the fact that the given calculation scheme defines the framework within which the algorithm operates. It can describe dependencies that occur in the real world solely by means of specific patterns. Simply put: more complex calculations provide an opportunity to solve more complicated problems.

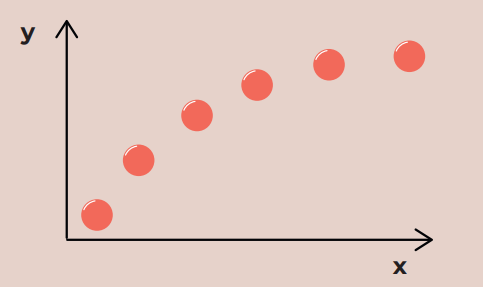
Figure 1. Collection of wind turbine performance measurements. One point is one measurement.

Let’s start by considering the example shown in Figure 1. Imagine that the chart shows a set of measurements of the efficiency of a wind turbine – one point represents one measurement. The x axis presents the wind speed, and the y axis displays the amount of energy generated by the turbine per minute at a specific wind speed. If we wanted to predict how much energy we will receive from a turbine over a specific time horizon, we would need a formula that described the relationship between these quantities. We could rely on the arrangement of points in the drawing and guess that it would be good to describe this relationship in the following way:

y = w₁ + w₂ * log(w₃ *x + w₄)

where w_i are the parameters. This is what a human-defined model could look like. Specific parameter values can be calculated during the learning process based on the values in the data (these are ready-made methods for calculating them). This description can be used to estimate y based on x. In other words: we will create a procedure that, for a given input value, will calculate the output size that interests us. This is precisely the approach that the main artificial intelligence algorithms are based on, especially the widely used algorithms for conducting conversations with humans.

They actually also convert text into numbers (we as users don’t see this), and their responses are the result of extremely complicated mathematical calculations. From the creators’ point of view, some fundamental questions arise: where do these formulas come from? Should we use a logarithm in the above example, or would it be better to go for a root? What patterns should we use if we want the algorithm based on them to be able to talk?

Guessing and manually selecting transformations (such as the appearing logarithms) can be applied in the calculations of different problems. It even has its advantages. However, in practice… It just doesn’t work often (e.g., because you have to perform a huge number of experiments to ensure a good-quality variant).
Sometimes this approach simply prevents achieving a high-quality solution. However, artificial intelligence would not have reached today’s level had it not been discovered long ago that modeling could be approached differently.

Artificial neural networks come to the rescue, standing behind all the biggest modern achievements in artificial intelligence. This is a major topic about which many books have been written. However, we will focus on the absolute basics, i.e., presenting the fundamental operational scheme that illustrates the essence of these algorithms. Remember that the type of network presented here is called a multilayer perceptron). It’s simply a set of patterns that can also be presented graphically (figure 2).

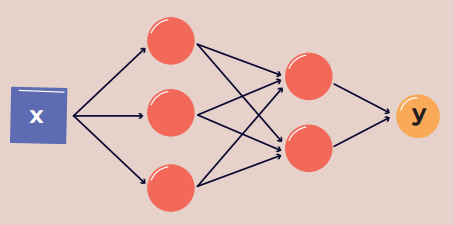
Figure 2. Multilayer perceptron

The square on the left side represents the input value – a number denoted as x, for which we want to know the network’s response. Each circle represents a neuron, which is a place where some value is calculated. The connections between elements show which values are transferred to which location, putting it simply, where they are further used in calculations. Each connection will have a specific weight assigned, which is a number that will be considered in the calculations. The value returned by the network is the value y calculated in the last neuron. Actually, we can talk about a layered arrangement here – the first layer is the first vertical row of three neurons, and the second is the second row with two neurons. That’s why we can call such a network two-layered.

In the description, we will use the following notations: x – input value, y – value returned by the network, n_i – values calculated in the neurons, w_i – weights assigned to connections, f – activation function, which can take different forms, but for the purposes of this example, let’s assume it will be the commonly used sigmoid function: f(z) = 1 / (1 + e^_-2), where e is Euler’s constant. Then, the network shown in Figure 2 can be described by the following calculation scheme:

n₁ = f(w₁ * x)

n₂ = f(w₂ * x)

n₃ = f(w₃ * x)

n₄ = f(w₄ * n₁ + w₅ * n₂ + w₆ * n₃)

n₅ = f(w₇ * n₁ + w₈ * n₂ + w₉ * n₃)

y = w₁₀ *n₄ + w₁₁ * n₅

This is a set of patterns that directly defines our algorithm, meaning it describes the relationships between the quantities x i y. Let’s note that specific values for the weights w_i are not determined by humans, but are selected during the network learning process. In other words, based on examples of real pairs (x, y), the network calculates by itself the weights for which it will most accurately guess y based on x. It is worth noting that the structure discussed here is purely exemplary, and in practice, a vast number of different variants are used, with the numbers of neurons and layers being very different. Additionally, neural networks can take multiple values as input (meaning they can estimate the quantity we’re interested in based on more than one input number). In practice, this is a typical situation (an example structure is shown in Figure 3).

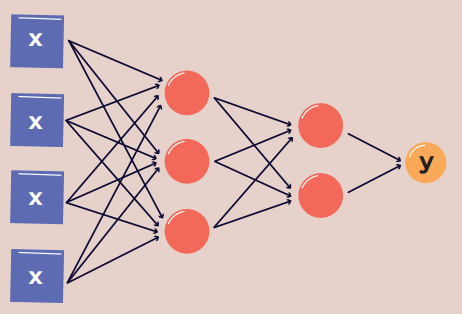
Figure 3. Neural network with four input values

TSuch defined algorithm is capable of describing very complex relationships and can handle solving many problems – especially those that cannot be solved by manually searching for the right formulas. In practice, the network’s performance will also depend on the choice of a specific structure, but in this case, a relatively small number of experiments will suffice. Importantly, depending on the specific weights, a network with the same structure can reflect relationships between x and y of very different shapes.
Thanks to this, the same model can be used for very different problems, which significantly facilitates the work of people creating solutions based on machine learning.

To conclude, let’s add that all major artificial intelligence algorithms are based on this very approach: whether we want to create an algorithm that detects objects in images or one that you can talk to, there are always sets of patterns designed by humans “under the hood”. It’s people who define their structure, but the exact values in equations (i.e., the mentioned parameters) are calculated during the algorithms’ learning process. In practice, much more complex structures of neural networks are used in many areas, and their design is handled by scientists. Ultimately, it’s us people who are behind the commonly used AI tools today.